Axiomatic System Of Geometry

The one and only interpretation in which its theorems are all true. In geometry a model of an axiomatic system is an interpretation of its primitives for which its axioms are true. Axiomatic SystemAxiomatic System An axiomatic system or axiom system includes. Such an axiom system is. An axiomatic system that is completely described is a special kind of formal system. Defined an axiomatic system is a set of axioms used to derive theorems. The lack of independence of the axiomatic system allows high school.

Give a short 5-10 min lecture on the history of Euclidean geometry its relevance in scientific and rational thinking and about axiomatic systems in general what they are and why they are important.

Present and discuss Euclids 23 definitions and five axioms. Properties Introduction Definition 5 An axiomatic system is categorical if every two models of the system are isomorphic. Axiomatic system designed for use in high school geometry courses. Give a short 5-10 min lecture on the history of Euclidean geometry its relevance in scientific and rational thinking and about axiomatic systems in general what they are and why they are important. W ecan v erify that an axiomatic system is complete b ysho wing that there is essen. Euclidean Geometry is an axiomatic system.

The Axiomatic System Definition Properties Video Lesson Transcript Study Com

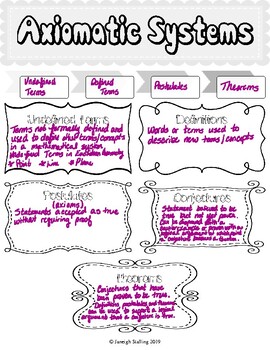
Axiomatic system of geometry. Object names but the objects they name are left unde ned. Thus the system consisting. Axiomatic system designed for use in high school geometry courses.

The primitives are Adaptation to the current course is in the margins. Eucliean and Non-Euclidean Geometry Fall 2007 Dr. What is an axiomatic system in geometry.

Undefined terms Axioms or statements about those terms taken to be true without ppproof. The axiom system includes the existence of a distance function coordinate functions and an angle measurement function. Here all the theorems are derived from the small number of simple axioms which are known as Euclidean geometry axioms.

The probably rst prototype of an axiomatic system can be found in Euclids Elements which present a systematic development of elementary geometry. Because these theorems are based on. The axiomatic system is a system of formal proofs.

An axiomatic system that is completely described is a special kind of formal system. W ecan v erify that an axiomatic system is complete b ysho wing that there is essen. The one and only interpretation in which its theorems are all true.

Also called postulates Theorems or statements proved from the axioms and previously proved theorems. Axiomatic Systems for Geometry George Francisy composed 6jan10 adapted 27jan15 1 Basic Concepts An axiomatic system contains a set of primitives and axioms. In mathematics the axiomatic method originated in the works of the ancient Greeks on geometry.

These derived statements are called the theorems of the axiomatic system. What this means is that for every theorem in math there exists an axiomatic system that contains all the axioms needed to prove that theorem.

Lesson 1 Axiomatic Systems And Incidence Geometry Outline

Example Of Axiomatic Systems Youtube

Lesson 1 Axiomatic Systems And Incidence Geometry Outline

Axiomatic Systems And Incidence Geometry Ppt Video Online Download

Ppt Axiomatic Systems Powerpoint Presentation Free Download Id 4520354

Ppt Axiomatic Systems Powerpoint Presentation Free Download Id 4520354

Axiomatic System2

Axiomatic System And Geometry 2018 2019 9292020 10

The Axiomatic System Definition Examples Video Tutors Com

What Is Axiomatic System What Does Axiomatic System Mean Axiomatic System Meaning Explanation Youtube

Ppt Geometry Axiomatic System Powerpoint Presentation Free Download Id 3809792

Line Non Euclidean Geometry Axiom Png 3780x2414px Noneuclidean Geometry Area Axiom Axiomatic System Diagram Download Free

Axiomatic System Png Images Pngwing

Mathematical System Axiomatic System Geometry Tagalog Youtube

13 Teaching Geometry Ideas Teaching Geometry Teaching Math Geometry

Axioms For Life

Formalization Of Notions In Affine Geometry Download Scientific Diagram

Introduction To Axiomatic Geometry By Mark Barsamian

Axiomatic System And Geometry 2018 2019 9292020 10

Tarski S Axioms Wikipedia

Math 3121 Abstract Algebra I Section 0 Sets The Axiomatic Approach To Mathematics The Notion Of Definition From The Text It Is Impossible To Define Ppt Download

Axiomatic System2

Section 2 2 Axiomatic Systems Math 333 Euclidean

Axiomatic System

Axiomatic Structure Of A Mathematical System In Geometry Math 8 Quarter 3 Module 2 Youtube

Lesson 1 Axiomatic Systems And Incidence Geometry Outline

Finite Geometries And Axiomatic Geometry Pages 1 4 Flip Pdf Download Fliphtml5

Axiomatic System An Overview Sciencedirect Topics

Axiomatic Systems And Incidence Geometry Ppt Video Online Download

Axiomatic Systems Youtube

Euclidean Geometry Wikipedia

Week 1 Axiomatic Systems Axiom Sets For Geometry Flashcards Quizlet

Section 2 2 Axiomatic Systems Math 333 Euclidean

Grade 8 Pdf Axiom Euclidean Geometry

Axiomatic System An Overview Sciencedirect Topics

Pdf An Axiomatic System For A Physical Or Digital But Continuous 3 Dimensional Euclidean Geometry Without Infinite Many Points

Lesson 1 Axiomatic Systems And Incidence Geometry Outline

Ns3 Balaroti Com Br

Modern Geom 1 Pdf Axiom Geometry

Axiomatic Systems Notes Handout By Jstalling Teachers Pay Teachers

Quiz Worksheet Properties Of The Axiomatic System Study Com

Absolute Geometry 978 613 5 77145 9 6135771450 9786135771459

2

An Axiomatic Approach To Geometry Springerprofessional De

Axiomatic System Png Images Pngwing

Solved 1 Consider The Following Axiomatic System A Ench Chegg Com

Mathematical System Axiomatic System Geometry Tagalog Youtube

Axiomatic System Msrblog

1

This is not the approach of Hilbert and of books that use Hilberts.

Here all the theorems are derived from the small number of simple axioms which are known as Euclidean geometry axioms. The probably rst prototype of an axiomatic system can be found in Euclids Elements which present a systematic development of elementary geometry. Properties Introduction Definition 5 An axiomatic system is categorical if every two models of the system are isomorphic. Object names but the objects they name are left unde ned. Axiomatic SystemAxiomatic System An axiomatic system or axiom system includes. 12 Axiomatic Systems in Propositional Logic 121 Description Axiomatic systems are the oldest and simplest to describe but not to use type of deductive systems. These derived statements are called the theorems of the axiomatic system. Thus the system consisting. Clearly the four axioms A1 A2 A3 and A4 form an inconsistent axiomatic system since we showed Theorem 3 that axioms A1 A2 A3 imply that any two lines have the same number of points contrary to A4.

Because these theorems are based on. The axioms are not independent of each other but the system does satisfy all the requirements for Euclidean geometry. Undefined terms Axioms or statements about those terms taken to be true without ppproof. Since a contradiction can never be true an axiom system in which a contradiction can be logically deduced from the axioms has no model. Eucliean and Non-Euclidean Geometry Fall 2007 Dr. A theory is a consistent relatively-self-contained body of knowledge which usually contains an axiomatic system and all its derived theorems. We know that the term Geometry basically deals with things like points line angles square triangle and other different shapes the Euclidean Geometry axioms is also known as the plane geometry.